Zadatak u nastavku je, navodno, u stanju da reši samo 2% ljudi na planeti.
Proverite da li ste među njima.
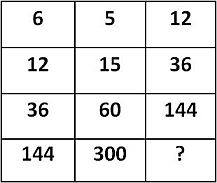
? + ? + ? =30
Umesto znakova pitanja koristi:
(1, 3, 5, 7, 9, 11, 13, 15)
Iste brojeve možeš koristiti više puta.
Ovo pitanje se pojavilo na finalnom ispitu na UPSC u decembru 2013 i samo je jedan student uspeo da ga reši (Gaurav Agarwal).
P.S. Dodatno zbunjuje (ili olakšava) to što je poznato da zbir tri neparna broja uvek bude neparan broj…